NumPy MedKit

A first-aid kit for the numerically adventurous

Stéfan van der Walt, University of Stellenbosch

Introduce yourself
- University of Stellenbosch, Department of Applied Mathematics
- Background is in engineering
- Developing NumPy is my PhD procrastination project
- Priviledged to be here with such talented people, many of whom could have been up here instead of me!, looking very much forward to the rest of this conference
Level of tutorial: "advanced track", but rather intermediate track
- Advanced topics may be of use to a select few, while I feel that these intermediate topics, while certainly not trivial, are common enough to warrant our attention.
Format of tutorial: challenge response
Read title, describe context, proceed to next slide

>>> import numpy as np
>>> np.random.seed([1, 2, 3])

A look inside our MedKit

Overview

Broadcasting

It is fundamental to NumPy array handling
Important, because it is so frequently used
- ... and abused!
Not a silver bullet to solve every problem (memory consumption)
Dispell some common misconceptions surrounding for-loops (more on that later)

Overview

Structured arrays

Common problem in industry: reading strange binary formats
- NumPy makes it easy!
Also a very convenient way of organising data
- Like columns in a spreadsheet

Overview

Views

Often, we repeatedly operate on the same values
- e.g. convolution, sliding window
- broadcasting
Views are a powerful way of reorganising data, without making copies
- Especially useful for large data-sets
Recently, Robert Kern added stride_tricks, with broadcast_arrays, as_strided.

Overview

Sub-classing

Before, sub-classing arrays used to be difficult and error-prone
- NumPy makes it a lot easier
Especially useful for adding meta-data, to be carried along with operations
- e.g. masked arrays, EXIF photographic tags, units, etc.
- Maybe a meta-data dictionary will be available in 2.0

Overview

(We'll skip this today)

Optimisation tricks

Talk about a few common pitfalls
Improving memory usage using for-loops
Profiling performance
Cython, ctypes example

Overview

Gems

If there's time left, chat about some hidden beauties:
- np.save and np.load
- np.fromregex
- np.lib.Arrayterator
- np.emath -- sqrt(-1)
- np.unravel_index
- np.lexsort and structured arrays
- np.iinfo
- np.issubdtype
- np.linalg.matrix_power

Broadcasting

Used to combine arrays of differing sizes
Simplest example: scalar broadcasting

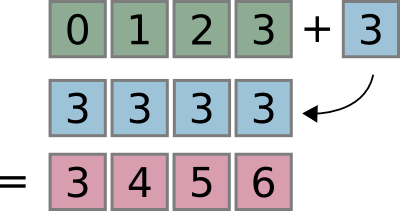
>>> x = np.arange(4)
>>> x
array([0, 1, 2, 3])
>>> x + 3
array([3, 4, 5, 6])

Broadcasting in 2D

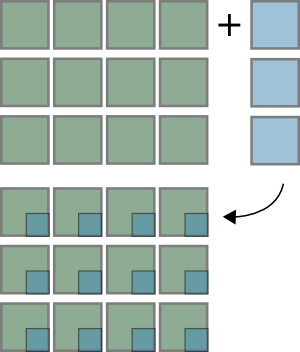
>>> x = np.zeros((3,4))
>>> y = np.zeros((3,1))
>>> (x + y).shape
(3, 4)

Broadcasting in 2D

Creating a grid of values:

>>> x, y = np.ogrid[1:10, 1:5]
>>> x
array([[1],
       [2],
       [3],
       [4],
       [5],
       [6],
       [7],
       [8],
       [9]])
>>> y
array([[1, 2, 3, 4]])
>>> x + 1j*y
array([[ 1.+1.j,  1.+2.j,  1.+3.j,  1.+4.j],
       [ 2.+1.j,  2.+2.j,  2.+3.j,  2.+4.j],
       [ 3.+1.j,  3.+2.j,  3.+3.j,  3.+4.j],
       [ 4.+1.j,  4.+2.j,  4.+3.j,  4.+4.j],
       [ 5.+1.j,  5.+2.j,  5.+3.j,  5.+4.j],
       [ 6.+1.j,  6.+2.j,  6.+3.j,  6.+4.j],
       [ 7.+1.j,  7.+2.j,  7.+3.j,  7.+4.j],
       [ 8.+1.j,  8.+2.j,  8.+3.j,  8.+4.j],
       [ 9.+1.j,  9.+2.j,  9.+3.j,  9.+4.j]])

Broadcasting in 2D

Timing two different approaches:

>>> def grid_old_way():
...     x, y = np.mgrid[1:100, 1:100]
...     return x + 1j*y

>>> def grid_new_way():
...     x, y = np.ogrid[1:100, 1:100]
...     return x + 1j*y

>>> timeit grid_new_way() 
1000 loops, best of 3: 301 µs per loop
>>> timeit grid_old_way() 
1000 loops, best of 3: 1.44 ms per loop

Broadcasting in 3D

>>> x = np.zeros((3, 5))
>>> y = np.zeros(8)
>>> (x[..., None] + y).shape
(3, 5, 8)

Broadcasting in N-D

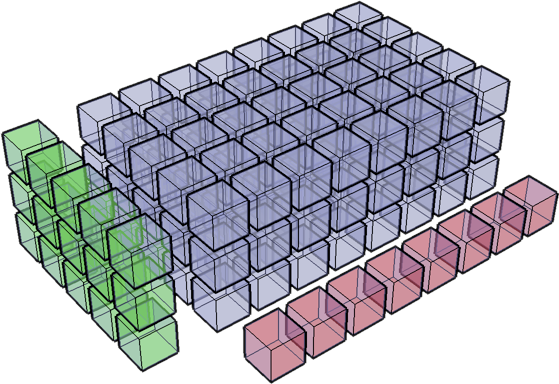
Compare dimensions, starting from last

Match when either dimension is one or None, or if dimensions are equal

Scalar    2D        3D            No go

( ,)      (3, 4)    (3, 5, 1)     (3, 5, 2)
(3,)      (3, 1)    (      8)     (      8)
----      ------    ----------    ---------
(3,)      (3, 4)    (3, 5, 8)        XXX

In action: vector quantisation

Code book: k M-dimensional data-points, as rows of (k, N) array
Given another set of data points of shape (m, N), for each find the closest point in the code book

>>> book = np.arange(1000).reshape(100,10)
>>> match = np.array([np.arange(100, 110),
...                   np.arange(155, 165),
...                   np.arange(173, 183)])

>>> for v in match:
...     min_dist = np.inf
...     for d in book:
...         dist = np.sum((v - d)**2)
...         if dist < min_dist:
...             best_match = d
...             min_dist = dist
...     print best_match, min_dist
[100 101 102 103 104 105 106 107 108 109] 0
[150 151 152 153 154 155 156 157 158 159] 250
[170 171 172 173 174 175 176 177 178 179] 90

Solution using broadcasting

>>> distances = (book - match[:, None, :])
>>> distances *= distances # square in-place
>>> distances = distances.sum(axis=2)
>>> chosen = distances.argmin(axis=1)
>>> book[chosen]
array([[100, 101, 102, 103, 104, 105, 106, 107, 108, 109],
       [150, 151, 152, 153, 154, 155, 156, 157, 158, 159],
       [170, 171, 172, 173, 174, 175, 176, 177, 178, 179]])
>>> distances[range(len(match)), chosen]
array([  0, 250,  90])

Not ideal -- the temporary array created has a large memory footprint:

(   100, 10)
(3,   1, 10)
------------
(3, 100, 10)

Usually, the number of vectors compared would be much greater, which exacerbates the problem.

Interlude: Indexing

Date: Wed, 16 Jul 2008 16:45:37 -0500
From: <Jack.Cook@>
To: <numpy-discussion@scipy.org>
Subject: [Numpy-discussion] Numpy Advanced
         Indexing Question

Greetings,

I have an I,J,K 3D volume of amplitude values
at regularly sampled time intervals. I have an
I,J 2D slice which contains a time (K) value at
each I, J location. What I would like to do is
extract a subvolume at a constant +/- K window
around the slice. Is there an easy way to do
this using advanced indexing or some other
method?  Thanks in advanced for your help.

- Jack

Indexing

Robert Kern responds:

cube[:, :, K-half_width:K+half_width]

But Jack's problem turned out to be a bit more tricky:

I can understand how this works if K is a constant
time value but in my case K varies at each
location in the two-dimensional slice. In other
words, if I was doing this in a for loop I would
do something like this

for i in range(numI):
  for j in range(numJ):
     k = slice(i,j)
     trace = cube(i,j,k-half_width:k+half_width)
     # shove trace in sub volume

Indexing

Indexing

First part of Robert's answer, shortened for tutorial purposes:

It would be great if you could just use slices
for the first two axes:

  cube[:, :, slice + numpy.arange(-half_width,
                                   half_width)]


but the semantics of that are a bit different
for reasons I can explain later, if you want.

Why doesn't this work?

Indexing

There are two ways of indexing NumPy arrays, using
- slices and scalars
- or ndarrays (known as fancy indexing)

>>> x = np.arange(9).reshape((3,3))
>>> x
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

>>> x[:, [0, 1, 2]]
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

>>> np.array([x[:, 0], x[:, 1], x[:, 2]])
array([[0, 3, 6],
       [1, 4, 7],
       [2, 5, 8]])

Indexing

Prepare Your Foil Deflector Beanies

Two-step process to predict the outcome:

Broadcast all index arrays against one another
Use the dimensions of the slices as-is

>>> x = np.random.random((15,12,16,3))
>>> index_one = np.array([[0, 1], [2, 3], [4, 5]])
>>> index_one.shape
(3, 2)
>>> index_two = np.array([[0, 1]])
>>> index_two.shape
(1, 2)

x[5:10, index_one, :, index_two].shape

Indexing

>>> x = np.random.random((15,12,16,3))
>>> index_one = np.array([[0, 1], [2, 3], [4, 5]])
>>> index_one.shape
(3, 2)
>>> index_two = np.array([[0, 1]])
>>> index_two.shape
(1, 2)

Broadcast index_one and index_two:

(3, 2)  # shape of index_one
(1, 2)  # shape of index_two
------
(3, 2)

Keeping this in mind, we may just be able to predict the following output:

>>> x[5:10, index_one, :, index_two].shape
(3, 2, 5, 16)

Indexing: Solve the problem

TIP: Use numpy.newaxis to change array dimensions to appease the Big Broadcaster.

>>> ni, nj, nk = (10, 15, 20)

# Make a fake data cube such that cube[i,j,k] == k for all i,j,k.
>>> cube = np.empty((ni,nj,nk), dtype=int)
>>> cube[:,:,:] = np.arange(nk)[np.newaxis, np.newaxis, :]

# Pick out a random fake horizon in k.
>>> kslice = np.random.randint(5, 15, size=(ni, nj))
>>> kslice
array([[ 6,  9, 11, 10,  9, 10,  8, 13, 10, 12, 13,  9, 12,  5,  6],
       [ 7,  9,  6, 14, 11,  8, 12,  7, 12,  9,  7,  9,  8, 10, 13],
       [10, 14,  9, 13, 12, 11, 13,  6, 11,  9, 14, 12,  6,  8, 12],
       [ 5, 11,  8, 14, 10, 10, 10,  9, 10,  5,  7, 11,  9, 13,  8],
       [ 7,  8,  8,  5, 13,  9, 11, 13, 13, 12, 13, 11, 12,  5, 11],
       [11,  9, 13, 14,  6,  7,  6, 14, 10,  6,  8, 14, 14, 14, 14],
       [10, 12,  6,  7,  8,  6, 10,  9, 13,  6, 14, 10, 12, 10, 10],
       [10, 12, 10,  9, 11, 14,  9,  6,  7, 13,  6, 11,  8, 11,  8],
       [13, 14,  7, 14,  6, 14,  6,  8, 14,  7, 14, 12,  8,  5, 10],
       [13,  5,  9,  7,  5,  9, 13, 10, 13,  7,  7,  9, 14, 13, 11]])

>>> half_width = 3

Indexing

# These two replace the empty slices for the first two axes.
>>> idx_i = np.arange(ni)[:, np.newaxis, np.newaxis]
>>> idx_j = np.arange(nj)[np.newaxis, :, np.newaxis]

# This is the substantive part that picks out the window
>>> idx_k = kslice[:, :, np.newaxis] + \
...         np.arange(-half_width, half_width+1) # (10, 15, 7)

cube[idx_i, idx_j, idx_k]

Apply the rule -- broadcast array indices, then add slices (but there are no slices in this case):

(ni,  1, 1                ) # idx_i
(1 , nj, 1                ) # idx_j
(ni, nj, 2*half_width + 1 ) # idx_k
---------------------------
(ni, nj, 7)

Phew, tough one. Moving on to easier things...

Indexing

>>> smallcube = cube[idx_i,idx_j,idx_k]
>>> smallcube.shape
(10, 15, 7)

# Now verify that our window is centered on kslice everywhere:
>>> smallcube[:,:,3]
array([[ 6,  9, 11, 10,  9, 10,  8, 13, 10, 12, 13,  9, 12,  5,  6],
       [ 7,  9,  6, 14, 11,  8, 12,  7, 12,  9,  7,  9,  8, 10, 13],
       [10, 14,  9, 13, 12, 11, 13,  6, 11,  9, 14, 12,  6,  8, 12],
       [ 5, 11,  8, 14, 10, 10, 10,  9, 10,  5,  7, 11,  9, 13,  8],
       [ 7,  8,  8,  5, 13,  9, 11, 13, 13, 12, 13, 11, 12,  5, 11],
       [11,  9, 13, 14,  6,  7,  6, 14, 10,  6,  8, 14, 14, 14, 14],
       [10, 12,  6,  7,  8,  6, 10,  9, 13,  6, 14, 10, 12, 10, 10],
       [10, 12, 10,  9, 11, 14,  9,  6,  7, 13,  6, 11,  8, 11,  8],
       [13, 14,  7, 14,  6, 14,  6,  8, 14,  7, 14, 12,  8,  5, 10],
       [13,  5,  9,  7,  5,  9, 13, 10, 13,  7,  7,  9, 14, 13, 11]])

>>> (smallcube[:,:,3] == kslice).all()
True

Structured Arrays

Structured Arrays

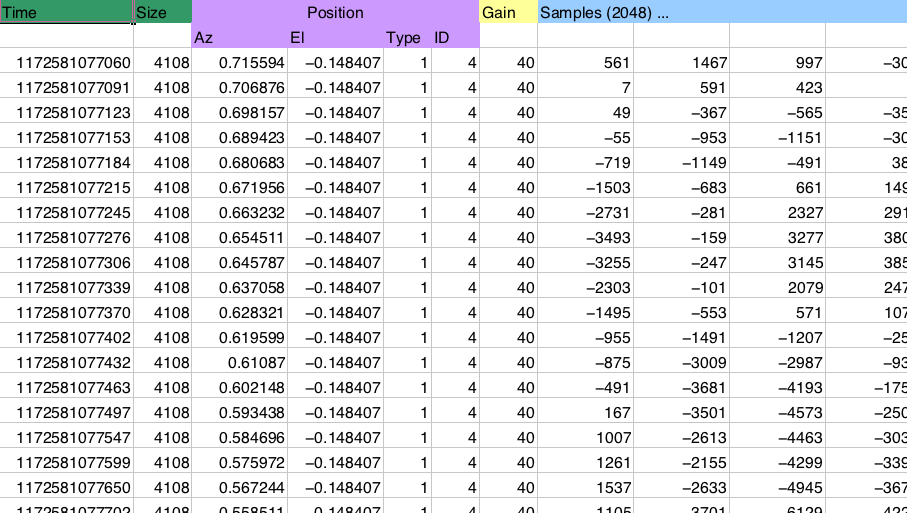
Reading this in most languages requires somewhat messy code. Not too bad, but not very pretty either:

while ((count > 0) && (n <= NumPoints))
  % get time - I8 [ms]
  [lw, count] = fread(fid, 1, 'uint32');
  if (count > 0) % then carry on
    uw = fread(fid, 1, 'int32');
    t(1,n) = (lw+uw*2^32)/1000;

    % get number of bytes of data
    numbytes = fread(fid, 1, 'uint32');

    % read sMEASUREMENTPOSITIONINFO (11 bytes)
    m(1,n) = fread(fid, 1, 'float32'); % az [rad]
    m(2,n) = fread(fid, 1, 'float32'); % el [rad]
    m(3,n) = fread(fid, 1, 'uint8');   % region type
    m(4,n) = fread(fid, 1, 'uint16');  % region ID
    g(1,n) = fread(fid, 1, 'uint8');

    numsamples = (numbytes-12)/2; % 2 byte integers
    a(:,n) = fread(fid, numsamples, 'int16');

Structured Arrays

The NumPy solution:

dt = np.dtype([('time', np.uint64),
               ('size', np.uint32),
               ('position', [('az', np.float32),
                             ('el', np.float32),
                             ('region_type', np.uint8),
                             ('region_ID', np.uint16)]),
               ('gain', np.uint8),
               ('samples', (np.int16,2048))])

data = np.fromfile(f, dtype=dt)

Access this data using dictionary-like syntax:

data['position']['az']

Views and strided tricks

Date: Wed, 16 Jul 2008 16:45:37 -0500
From: Amir
To: <numpy-discussion@scipy.org>
Subject: [Numpy-discussion] interleaved
         indexing

A very beginner question about indexing: let x be
an array where n = len(x). I would like to create
a view y of x such that:

y[i] = x[i:i+m,...]  for each i and a fixed m << n

so I can do things like numpy.cov(y). With n
large, allocating y is a problem for
me. Currently, I either do for loops in cython or
translate operations into correlate() but am
hoping there is an easier way, maybe using fancy
indexing or broadcasting. Memory usage is
secondary to speed, though.

Views and strided tricks

Given input data:

>>> x = np.arange(20).reshape([4, 5])
>>> x
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])

What he wants is a view like this (assume m == 2):

array([[[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9]],

       [[ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14]],

       [[10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]]])

Views and strided tricks

To do this, we need to know the following terms:

shape: The dimensions of the array along each axis.
strides: The number of bytes of memory that must be skipped to progress to the next item along a certain dimension.

>>> x.strides
(20, 4)

>>> np.int32().itemsize
4

Views and strided tricks

array([[[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9]],

       [[ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14]],

       [[10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]]])

We now need to manipulate the array shape and strides. The output shape must be (3, 2, 5), i.e. 3 items, each containing two rows (m == 2), and each row having 5 elements.

The strides need to change from (20, 4), to (20, 20, 4). Each item in the new output array starts at a new row, that each row consists of 20 bytes (5 elements of 4 bytes each), and each element occupies 4 bytes (int32).

Views and strided tricks

Let's do it:

>>> from numpy.lib import stride_tricks
>>> stride_tricks.as_strided(x, shape=(3, 2, 5),
...                             strides=(20, 20, 4))
array([[[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9]],

       [[ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14]],

       [[10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]]])

Views and strided tricks

Or the old way (which is basically what as_strided does under the hood):

>>> d = dict(x.__array_interface__)
>>> d['shape'] = (3, 2, 5)
>>> d['strides'] = (20, 20, 4)

>>> class Arr:
...     __array_interface__ = d
...     base = x

>>> np.array(Arr())
array([[[ 0,  1,  2,  3,  4],
        [ 5,  6,  7,  8,  9]],

       [[ 5,  6,  7,  8,  9],
        [10, 11, 12, 13, 14]],

       [[10, 11, 12, 13, 14],
        [15, 16, 17, 18, 19]]])

Subclassing

Two important methods:

__new__: Allocated memory for ndarray object; only called when new array is created (i.e. not view).
__array_finalize__: Called to setup an array or view, whether or not __new__ was invoked.

Subclassing

class InfoArray(np.ndarray):

    def __new__(subtype, data, info=None, dtype=None, copy=False):
        subarr = np.array(data, dtype=dtype, copy=copy)
        subarr = subarr.view(subtype)

        if info is not None:
            subarr.info = info
        elif hasattr(data, 'info'):
            subarr.info = data.info

        return subarr

    def __array_finalize__(self, obj):
        self.info = getattr(obj, 'info', {})

In conclusion

I would like to thank

Enthought, for generously sponsoring my visit, and for being one of the pillars of this community
My study advisor, Ben Herbst, who doesn't ask too many questions when I disappear for a month
You, for taking the time to attend this talk

NumPy MedKit

SciPy Conference • 08-2008

NumPy MedKit

A first-aid kit for the numerically adventurous

A look inside our MedKit

Overview

Overview

Overview

Overview

Overview

Overview

Broadcasting

Broadcasting in 2D

Broadcasting in 2D

Broadcasting in 2D

Broadcasting in 3D

Broadcasting in N-D

In action: vector quantisation

Solution using broadcasting

Interlude: Indexing

Indexing

Indexing

Indexing

Indexing

Indexing

Indexing

Indexing: Solve the problem

Indexing

Indexing

Structured Arrays

Structured Arrays

Structured Arrays

Views and strided tricks

Views and strided tricks

Views and strided tricks

Views and strided tricks

Views and strided tricks

Views and strided tricks

Subclassing

Subclassing

In conclusion